Latest revision as of 15:46, 30 December 2022

@@ Line 1: / Line 1: @@
-=Definition=
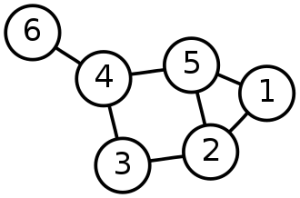
+[[File:Graph2.png|thumb|Graph with 6 [[Vertex|vertices]] and 7 [[edge]]s.]]
-A graph is a structure amounting to a set of [[concept]]s in which some pairs of these concept are related.
-<ref>Wikipedia: Graph (discrete methematics). [https://en.wikipedia.org/wiki/Graph_(discrete_mathematics)]</ref>
-=Generic relations=
+=[[Definition]]=
+A graph is a structure amounting to a set of [[Vertex|vertices]] in which some pairs of these [[edge]]s have a [[relation]]ship.
+<ref>Wikipedia.  [https://en.wikipedia.org/wiki/Graph_(discrete_mathematics) Graph (discrete methematics).]</ref>
+=[[Synonym]]s=
+* Network
+=[[Generic relation]]s=
 In [[Generic relation]]s. [[superordinate concept]]s and [[subordinate concept]]s can be distinguished:
@@ Line 9: / Line 14: @@
 * Structure
-[[Subordinate concept]]a A are:
+[[Subordinate concept]]s A are:
-* Directed graph
+* [[Directed graph]]
 * Mixed graph
 * Weighted graph
@@ Line 27: / Line 32: @@
 * Poly tree
 * Advanced kinds of graphs
-[[File:Graph2.png|thumb|Graph with 6 vertices and 7 edges.]]
-=Partitive relations=
+=[[Partitive relation]]s=
-In [[Partitive relation]]s, [[superordinate concept]]s and [[subordinate concept]]s can be distinguished:
 [[Subordinate concept]]s (parts) are:
-* Vertex
+* [[Triple]]
-* Edge
+** [[Vertex]]
+** [[Edge]]
-=References=
+=[[Reference]]s=
 [[Category:All]]

Graph: Difference between revisions