Graph: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
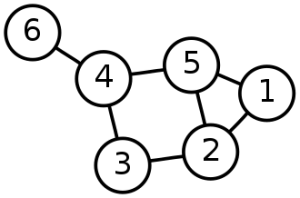
=Definition= | [[File:Graph2.png|thumb|Graph with 6 [[Vertex|vertices]] and 7 [[edge]]s.]] | ||
=[[Definition]]= | |||
A graph is a structure amounting to a set of [[Vertex|vertices]] in which some pairs of these [[edge]]s have a [[relation]]ship. | A graph is a structure amounting to a set of [[Vertex|vertices]] in which some pairs of these [[edge]]s have a [[relation]]ship. | ||
<ref>Wikipedia | <ref>Wikipedia. [https://en.wikipedia.org/wiki/Graph_(discrete_mathematics) Graph (discrete methematics).]</ref> | ||
=Synonym= | =[[Synonym]]s= | ||
* Network | * Network | ||
=Generic | =[[Generic relation]]s= | ||
In [[Generic relation]]s. [[superordinate concept]]s and [[subordinate concept]]s can be distinguished: | In [[Generic relation]]s. [[superordinate concept]]s and [[subordinate concept]]s can be distinguished: | ||
| Line 30: | Line 32: | ||
* Poly tree | * Poly tree | ||
* Advanced kinds of graphs | * Advanced kinds of graphs | ||
=[[Partitive relation]]s= | |||
[[Subordinate concept]]s (parts) are: | [[Subordinate concept]]s (parts) are: | ||
* [[Triple]] | * [[Triple]] | ||
| Line 40: | Line 39: | ||
** [[Edge]] | ** [[Edge]] | ||
= | =[[Reference]]s= | ||
[[Category:All]] | [[Category:All]] | ||
Latest revision as of 15:46, 30 December 2022
Definition
A graph is a structure amounting to a set of vertices in which some pairs of these edges have a relationship. [1]
Synonyms
- Network
Generic relations
In Generic relations. superordinate concepts and subordinate concepts can be distinguished:
- Structure
Subordinate concepts A are:
- Directed graph
- Mixed graph
- Weighted graph
Subordinate concepts B are:
- Oriented graph
- Regular graph
- Complete graph
- Finite graph
- Connected graph
- Bipartite graph
- Path graph
- Planar graph
- Cycle graph
- Tree
- Poly tree
- Advanced kinds of graphs
Partitive relations
Subordinate concepts (parts) are:
References
- ↑ Wikipedia. Graph (discrete methematics).